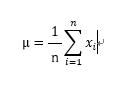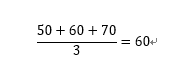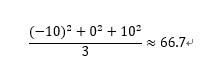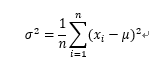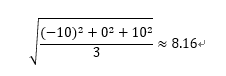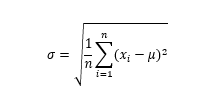受験の難易度を示す指標として一般的に用いられる偏差値。
上がったり下がったりする偏差値に一喜一憂している受験生は多いと思います。
しかし、実際どういう原理で偏差値が求められるのかを知っている人は意外と少ないのではないでしょうか？
偏差値は、平均点や点数のばらつき具合などが違う試験でも、相対的な成績の良さを比較できる便利な指標です。
この記事では、偏差値の求め方と原理をご紹介します。

多くの場合、テストの成績は平均点に近い点数の人が一番多く、平均点から離れれば離れるほど人数が減っていきます。

こういった左右対称の釣鐘型の分布の仕方を、「正規分布」と呼びます（※1）。
テストの点数だけでなく、体重や身長など多くの分布でも、平均に近いほど高くなり、両側に向かってだんだん低くなる、正規分布になることが知られています。
それに対して、市町村ごとの人口の分布などは、人口の多い市はほんの一握りで、ほとんどの市町村ではわずかな人口差で並ぶ、大きく偏った分布を示します。
この分布は正規分布に対して「べき分布」とよばれ、正規分布と同じくらいよく見られるものです。
SNSの友達数や、ショッピングサイトの売り上げなども、べき分布にあてはまります（※2）。

他にも、分布の山が2つ以上現れる場合があります。

これは、二峰性分布と呼ばれる分布で、正規分布やべき分布ほど一般的ではありませんが、2つの異なる集団が混ざっている場合に生じやすいです。
例えば、握力などでは女性と男性では平均値がかなり違うため、男女それぞれの分布自体は正規分布に従っていても、両方を合わせた分布の形を見ると、女性の平均値付近のピークと男性の平均値付近のピークという、2つの山が出てきます（※3）。

このように、データのばらつき具合（分布）の形はさまざまで、いくつかの形に分類されています。

偏差値を求める大前提として、そのテストを受けた人の点数が正規分布に従う必要があります（※4）。
定期テストなどでは少人数のクラス内での偏差値が算出されることがありますが、人数が少ない場合には成績の分布がこの正規分布に従わないこともあります。
そういった場合には、数値として偏差値が示されていても、それが信頼の置ける値であると言えないので注意が必要です。

※1：総務省統計局　なるほど統計学園高等部　「正規分布」／　2018年2月15日現在
https://www.stat.go.jp/koukou/howto/process/p4_3_2_1.html
※2：ヤフー株式会社　Yahoo! JAPANビッグデータレポート　「ビッグデータも自然現象の法則から逃れられないという一つの発見」／　2018年2月15日現在
https://about.yahoo.co.jp/info/bigdata/special/2016/03/
※3：統計WEB STEP 1. 基礎編　「3-3. 平均・中央値・モードの使い方」／　2018年2月15日現在
https://bellcurve.jp/statistics/course/4322.html
※4：総務省統計局　なるほど統計学園高等部　「偏差値」／　2018年2月15日現在
https://www.stat.go.jp/koukou/howto/process/p4_3_2_2.html

偏差とは、各受験者の点数から平均点を引いた値のことを指します。
偏差値と似た言葉ですが、一字違うだけで全く違う意味なので注意しましょう。

偏差値を求めるためには、まず標準偏差と呼ばれる数値が必要となります。
標準偏差を求めるためには、まず平均と分散を求める必要があります。
おそらく多くの人が知っている通り、平均は、全員の点数の合計を受験した人数で割った数値です。
平均μを式で示すと、下記の通りになります。

（ただしnは受験者数、x_iは各人の点数）

たとえば、Aさん、Bさん、Cさんの点数がそれぞれ、50点、60点、70点だった場合、平均点は、

で、60点となります。

次に、分散についてです。
分散とは、その名前が示す通り、データの散らばり具合を示す指標のことで、散らばり具合が大きいほど分散も大きくなります。
そのため、ほとんどの人が平均点に近い点数を取っている場合は、分散が小さくなります。
それに対して、平均点に近い点数の人は多いものの分布の山はなだらかで、平均よりもずっと良い、あるいは悪い点数の人もそれなりにいる場合は、分散が大きくなります。

では、実際に数値として分散を求めるためには一体どうしたら良いでしょうか。
そのためには、まず「平均値と一人一人の点数との離れ具合」、つまり偏差を知る必要があります。

さきほどのAさん、Bさん、Cさんの例で見ると、平均点は60点なので、３人の偏差はそれぞれ次の通りになります。

つぎに、こうして得られたひとりひとりの偏差を２乗した値の合計を求めます。
Aさん、Bさん、Cさんの偏差の２乗の合計は、下記の通りです。

偏差を２乗する理由は、平均値よりも低い点数の人の場合は数値がマイナスになってしまうからです。
点数は正規分布に従うと仮定すると、平均値よりもN点低い人と、平均値よりN点高い人の数は同じなので、そうするとそれぞれの受験者の点数と平均値との差の合計が相殺されてゼロになってしまい、これではばらつき具合を見ることができません。
そこで、２乗することによって、平均値からのばらつき具合の合計が算出できるわけです。

しかしこのままですと、受験者数が多ければ多いほど数値が大きくなってしまうので、異なる試験同士でばらつきの差を比べることはできません。
そこで、さきほどの計算で得られた数値を受験者数で割ります。
つまり、偏差の２乗の平均値ということです。
こうして求められた数値が、分散です。
したがって、Aさん、Bさん、Cさんの偏差の分散は、下記の通りになります。

分散σ2を数式で示すと、下記の通りになります。

（ただしnは受験者数、x_iは各人の点数、μは平均値）

こうして求められた分散の正の平方根（ルート）が、標準偏差と定義されています。
したがって、Aさん、Bさん、Cさんの偏差の標準偏差は、下記の通りになります。

わざわざ平方根にするのには、分散を求める際に、平均値より低い人の偏差がマイナスになってしまうため、偏差を2乗した値を計算に用いたことと関係しています。

偏差自体は平均点との差という「点数」で示すことができる数値でしたが、分散はこの偏差を2乗するという処理が入ってしまっているので、点数とは比較できないほど大きな数値になってしまいます。
ざっくりいうと、分散の平方根を求めるのは、2乗して大きくなりすぎた数値を再び同じ点数という土俵に引き戻すためなのです。
標準偏差σは数式で示すと次の通りとなります。

（ただしnは受験者数、x_iは各人の点数、μは平均値）

表1. 標準偏差を求める流れ

（ただしnは受験者数、x_iは各人の点数、μは平均値、σは標準偏差）

Aさん、Bさん、Cさんの3人の試験で、実際に計算で分散と標準偏差を求めて、全体のイメージをつかみました。
しかし実際にはたった3人しか受けていない試験というのはまれですし、上述の通り偏差値を求める前提として点数が正規分布に従う必要があるため、３人では分布の形を特定することはできないので、偏差値を一応算出することはできるものの、前提を満たしていない以上それは信頼できる数値とは言えません。

そこで、もっと受験人数の多い現実的な例を見ていきましょう。
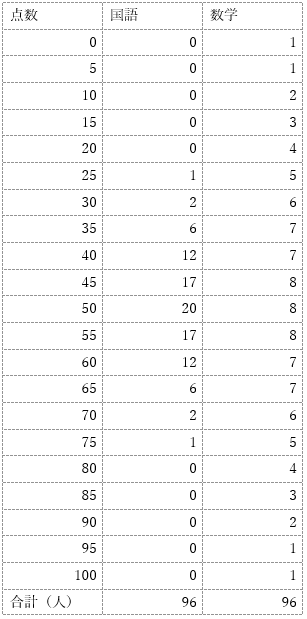
たとえば、96人の学年で、1問5点の配点で、全部で20問ある100点満点の国語と数学のテストがあり、各点数の人数は下記の通りだったとします。

表2.  国都と数学の点数分布

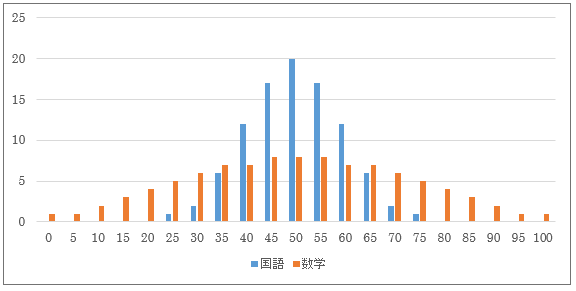
これをグラフにすると、下記のように、国語も数学も正規分布に従いますが、点数の散らばり具合が全く違うことがわかります。

国語は平均点近くの人が集中しているのに対して、数学では平均点を中心になだらかな分布となっています。

図1. 国語と数学の得点分布。２科目とも平均点は50点だが、分布の形は全くちがう。

では、国語と数学の標準偏差をまず計算してみましょう。
まずは国語です。
国語の平均点は、

(25×1+30×2+35×6+40×12+45×17+50×20+55×17+60×12+65×6+70×2+75×1)/96 = 50

で、50点となります。

次に、分散は、

{(25-50)2×1+(30-50)2×2+(35-50)2×6+(40-50)2×12+(45-50)2×17+(50-50)2×20+(55-50)2×17+(60-50)2×12+(65-50)2×6+(70-50)2×2+(75-50)2×1)}/96 ≒ 91.67

となります。

よってその平方根である標準偏差は、

√91.67≒9.57

となります。

それに対して数学の平均点は、

(0×1+5×1+10×2+15×3+20×4+25×5+30×6+35×7+40×7+45×8+50×8+55×8+60×7+65×7+70×6+75×5+80×4+85×3+90×2+95×1+100×1)/96 = 50

と、国語と同じ50点です。

しかし分散は、

{(0-50)2×1+(5-50)2×1+(10-50)2×2+(15-50)2×3+(20-50)2×4+(25-50)2×5+(30-50)2×6+(35-50)2×7+(40-50)2×7+(45-50)2×8+(50-50)2×8+(55-50)2×8+(60-50)2×7+(65-50)2×7+(70-50)2×6+(75-50)2×5+(80-50)2×4+(85-50)2×3+(90-50)2×2+(95-50)2×1+(100-50)2×1)/96 ≒479.17

となります。

よって数学の標準偏差は、

√479.17 ≒ 21.89

となり、国語の9.57の倍以上のばらつきを示していることがわかります。

このように、国語と数学は平均点だけをみても違いがわかりませんが、分散や標準偏差という散らばり具合の指標を見ると数学の方が大きく、分布図で見た通り違いを反映していることがわかります。

それでは、いよいよ偏差値の求め方を見ていきましょう。

偏差値50、というのは平均的な成績を指すことは知られていますが、それは実は、平均が50になるように偏差値が定義されているからです。
まず、個人の得点と平均値との差を求め、それを標準偏差で割ります。
そうして得られた数値の平均は0、標準偏差は1になります。

これは、それぞれに平均やばらつき具合が違う分布を、比較できるように同じ平均値・標準偏差に変換する作業で、標準化と言います。
そして、この標準化した値を10 倍して、50を足した数が偏差値です。
偏差値yは、数式で示すと、下記の通りになります（※1）。

（ただし、x_iは各人の点数、μは平均値、σは標準偏差）

・「偏差値50」が平均なのは、平均が50になるように偏差値が定義されているから

これに従って、先ほどの国語と数学で75点の人の偏差値を求めてみると、
国語の場合は、

50+10×(75-50/9.57) ≒76

数学の場合は、

50+10×(75-50/21.89) ≒61

となります。

このように、同じ75点であっても、数学の偏差値は約61、国語は約76と、国語の方が圧倒的に偏差値の高いことがわかります。

※1：総務省統計局　なるほど統計学園高等部　「偏差値」／　2018年2月15日現在
https://www.stat.go.jp/koukou/howto/process/p4_3_2_2.html

先ほどの国語と数学の例を見てみても、数学ならば75点以上取っている人は少なくはないのに対し、国語は75点が最高点ですので、感覚的に「国語の75点の方がすごい」というのは、誰でも直感では理解できると思います。
しかし、平均点は同じ50点なので、平均点との差だけを見ていても、どのくらい75点という点数が良い成績なのかを、客観的な数値として確認することはできません。
ところが、それぞれの偏差値を求めることで、違う試験でも客観的な成績の良さを比較できるようになります。

つまり、わざわざ偏差値を求めるメリットは、平均点や得点の散らばり具合に違いがあるテストや科目でも相対的な成績の良さを比較することができるようになることです。

これまでご紹介してきたように、偏差値は平均値や分散といって数値に基づいて求められますので、テストを受けた人の点数分布の形や平均点に大きく左右されます。
そのため、「◯◯大学△△学部は偏差値60くらい」というような表現をされることが多いですが、実際は試験によって目安となる偏差値は変わってきます。
たとえば大手の予備校では、「〇〇大学模試」など、特定の大学を受験する人にターゲットを絞った模試を実施しており、難関大学模試では、普通の模試より偏差値が低く出やすくなります。
また大規模な全国模試などですと、同じ学校を志望する人の中での偏差値が出ることもあり、その場合も同様に偏差値は高くなりにくいです。
これは、その試験を受ける人がすでにその難関大学を志望校として勉強していてレベルが高いためです。

今はスマホやパソコンなどで簡単に志望校の合格ラインと言われる偏差値を調べることができます。
しかし、どの試験でもその偏差値が要求されるわけではありません。
試験を受けるたびに偏差値が変動すると、つい一喜一憂してしまうものですが、試験を受けている母集団に大きく左右されることを頭の片隅において、あまり偏差値に振り回されないようにしましょう。

偏差値は一般的な言葉ですが、求め方を知らない人も多かったのではないでしょうか。
受験勉強の合間に数学の復習がてら、自分の偏差値を手計算で求めてみてもいいのではないでしょうか。
また、偏差値の求め方は、数学の中でも特に社会で活躍することが多い「統計学」の考え方のエッセンスが詰まっています。
文系なので数学は関係ない、と思っている方も多いですが、統計学は客観的に差があるといえるかどうかを示す強力なツールです。
将来就職したあと、売り上げのデータなどをみる機会は文系の方でも多いはずです。
この機会に、偏差値の求め方を通じて統計の考え方の一端に触れておくことは将来の役に立つのではないでしょうか。